Sorting algorithms are a fundamental aspect of computer science, used to arrange data in a particular order. There are many different sorting algorithms, each with its own strengths and weaknesses. The choice of an algorithm often depends on the specific requirements of the problem at hand. In this topic, we'll delve into sorting algorithms, exploring the steps involved in each algorithm, how they can be used to solve real-world problems, and their strengths and weaknesses. With a solid understanding of sorting algorithms and their applications, you'll be equipped to tackle a wide range of data sorting problems, from simple sorting tasks to complex data analysis projects.

Basics of sorting algorithms

Understanding the basics of sorting algorithms is a great starting point. Here's a closer look at the different types of algorithms and the basic principles behind each one:

Comparison-based sorting algorithms — these algorithms sort data by comparing elements to one another. The most common comparison-based sorting algorithms include bubble sort, insertion sort, selection sort, merge sort, and quick sort.
Non-comparison-based sorting algorithms — these algorithms sort data without comparing elements to one another. Instead, they rely on mathematical properties of the data, such as its distribution or range, to sort the data. An example of a non-comparison-based sorting algorithm is counting sort.

The basic principle behind all sorting algorithms is to arrange data in a particular order, such as ascending or descending. This is achieved by comparing a range of elements to one another and swapping them as necessary to achieve the desired order. When comparing different sorting algorithms, it's helpful to group them by their time complexity and their practical applications. Time complexity refers to how the sorting algorithm performs as the size of the dataset increases. Practical applications refer to the types of datasets and the contexts in which the sorting algorithm is most useful.

One way to visualize the advantages and disadvantages of different sorting algorithms is to create a table or a chart that compares them based on different criteria. For example, we could create a table that compares the time complexity of each algorithm, the memory requirements, and the suitability for different types of datasets.

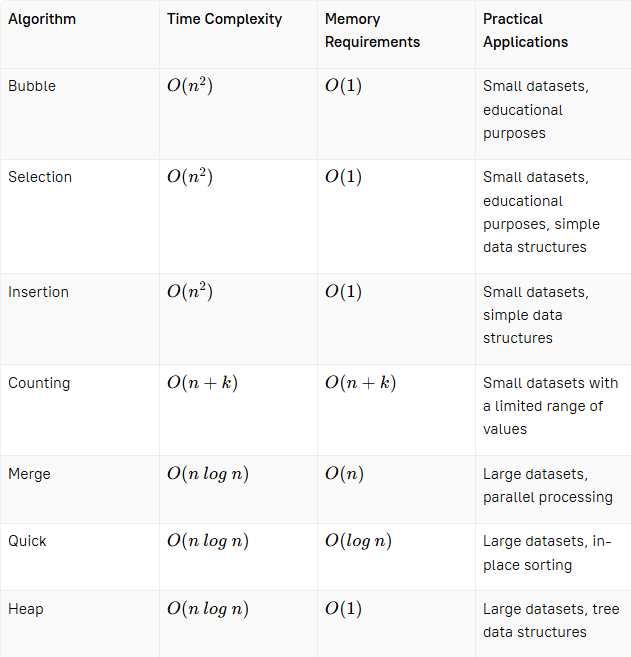
This table shows that bubble sort and insertion sort are suitable for small datasets and educational purposes. Merge sort, quick sort, and heap sort are suitable for larger datasets and more complex data structures. Merge sort and quick sort have the advantage of being efficient for parallel processing, while quick sort is an in-place sorting algorithm, which means it requires no additional memory. The counting sort has a time complexity of O(n+k), where k is the range of values in the input. This makes it ideal for sorting small datasets with a limited range of values, such as integers between 0 and 100. Counting sort requires additional memory to store the counts of each value, so it's not ideal for very large datasets.

It's important to note that each algorithm has its own strengths and weaknesses, and the choice of sorting algorithm depends on the specific requirements of the problem. For example, if the input data is already partially sorted, insertion sort may be the best choice, as it has a time complexity of O(n) in the best-case scenario. Conversely, if the input data is mostly random, quick sort may be a better choice as it has an average time complexity of O(nlogn).

When to use a particular sorting algorithm

To choose an appropriate sorting algorithm for a problem, we need to consider the properties of the problem. Here are some general rules to follow:

If the data set is small, use bubble sort, insertion sort, or selection sort.
If the data set is large and unsorted, use merge sort or quick sort.
If the data set has a limited range of values, use counting sort.
If the data set is already partially sorted or has many duplicate values, use insertion sort or merge sort.
If memory is limited, consider using an in-place sorting algorithm like quick sort or heap sort.

Let's consider some examples to see how these rules apply in practice.

Example 1: sorting a large database

Suppose we have a large database of customers that we want to sort by last name. The database contains millions of records. In this case, merge sort or quick sort would be the best choice since the dataset is large.

Example 2: sorting a list of floating-point numbers

Suppose we have a list of floating-point numbers that we want to sort in ascending order. The list contains 5000 elements, each within the range of 0 to 999. Due to the nature of floating-point arithmetic, we cannot use comparison-based sorting algorithms such as merge sort or quick sort because they require strict ordering of elements. Instead, we can use counting sort, a non-comparison-based sorting algorithm, to sort the list in O(n+k) time, where n is the number of elements and k is the range of input elements. In this case, we would need to create a counting array of size 1000 to keep track of the frequency of each integer in the input list. Once we have the frequency counts, we can use them to generate a sorted list of integers in ascending order.

Example 3: sorting a list of strings by length

Suppose we have a list of strings that we want to sort by length in ascending order. The list contains 1000 elements. We can use any comparison-based sorting algorithm for this problem, but since we are sorting by length, we can use a modified version of quick sort that chooses the pivot based on the length of the strings rather than their values. This approach is called quick sort with median-of-three partitioning and has a time complexity of O(nlogn) in the average case.

Example 4: sorting an array in descending order

Suppose we have an array of integers that we want to sort in descending order which contains only 20 elements. We can use any sorting algorithm for this problem since the dataset is small. However, since we want to sort the array in descending order, we need to use a sorting algorithm that can be modified to sort in reverse order, such as merge sort or quick sort. By modifying these algorithms, we can transform the original array into a sorted array by changing the comparison operator to sort the elements in reverse order.

Example 5: sorting a list of objects by a property

Suppose we have a list of objects that we want to sort by a specific property in descending order. The list contains 100 elements. We can use any comparison-based sorting algorithm for this problem, but since we are sorting by a specific property, we can use a modified version of selection sort that compares objects based on the desired property rather than their values. This approach is called selection sort with comparator and has a time complexity of O(n^2) in the worst case. Alternatively, we can use a stable sorting algorithm such as insertion sort or merge sort if we want to preserve the relative order of equal elements based on their original order in the input.

Example 6: sorting a large dataset

Let's say we have a large dataset consisting of integers, and we need to sort them in ascending order. The dataset contains duplicates, and we need to remove them while sorting. In this case, we would choose the quick sort algorithm. Quick sort is a fast sorting algorithm that can efficiently sort large datasets. Additionally, it has the advantage of being an in-place sorting algorithm, which means it does not require additional memory to sort the data. Quick sort also has low memory overhead, making it an ideal choice for datasets that cannot be loaded into memory all at once. To remove duplicates, we would modify the quick sort algorithm to check for duplicates while sorting. If duplicates are found, they are removed. This can be accomplished by keeping track of the last non-duplicate element during the sort and only swapping elements if the current element is not equal to the last non-duplicate element. In this scenario, we would choose quick sort because of its efficiency in sorting large datasets, its low memory overhead, and its ability to be modified to remove duplicates while sorting. Other sorting algorithms such as bubble sort or insertion sort would not be appropriate as they are slower and have higher memory overheads.

Sorting Example for Java

Let's analyze why Java uses quick sort for primitive types and merge sort for reference types.

In Java, the built-in sorting algorithm uses quick sort for primitive types and merge sort for reference types. This built-in method is chosen based on the characteristics of the data types being sorted. Quick sort is often faster for small data sets, while merge sort is better suited for larger data sets. In addition, quick sort is an in-place algorithm, meaning that it can sort the data in the same memory space, which is more memory efficient for small data sets. On the other hand, merge sort method requires additional memory for the merge step, making it more efficient for larger data sets.

The stability of the sorting algorithm is another important factor to consider. A stable sort algorithm maintains the relative order of equal elements in the original data set, which is important in some use cases. For primitive types, however, stability is not a concern since they do not have any inherent ordering beyond their numerical value. Therefore, quick sort is chosen for its efficiency and in-place sorting capability.

In contrast, reference types such as objects have a more complex internal structure, and their sorting may depend on multiple attributes. Therefore, it is important to preserve the relative order of equal elements when sorting reference types. Merge sort is a stable algorithm and can guarantee the preservation of the relative order of equal elements.

It's worth noting that the choice of algorithm can affect the efficiency of sorting for different data sizes. The summary table suggests that both quick sort and merge sort are efficient for large data sets, but in reality, their efficiency may depend on the specific implementation and the characteristics of the data being sorted. For example, in the case of a linked list, it may be possible to perform merge sort without allocating additional memory. Similarly, quick sort may require additional memory if the recursion depth becomes too large. Therefore, it's important to carefully consider the characteristics of the data being sorted when selecting a sorting algorithm.

By understanding the factors that influence the choice of sorting algorithm, you can make more informed decisions when processing data sets in your programming projects.

Real-life applications

One real-life scenario where we could compare different sorting algorithms is in the processing of large data sets in scientific research.

For example, let's say a research lab has collected data from a study involving thousands of subjects, and they need to sort the data by various criteria such as age, gender, and health status. The lab may need to perform this sorting repeatedly as they analyze the data and make new discoveries.

In this scenario, the choice of sorting algorithm can make a significant difference in terms of the time and resources required to perform the sorting. If the data set is relatively small, a simple algorithm like bubble sort or insertion sort may be sufficient. However, if the data set is very large, a more efficient algorithm like merge sort or quick sort may be necessary.

Let's assume that the data set in this scenario is very large, consisting of millions of data points. In this case, using an inefficient sorting algorithm like bubble sort or insertion sort would take an unacceptably long time to sort the data. Instead, the research lab may choose to use a more efficient algorithm like merge sort or quick sort. These algorithms have a time complexity of O(nlogn), which means they can sort the data in a reasonable amount of time.

However, even within the category of O(nlogn) algorithms, there are differences in efficiency and memory usage. For example, merge sort requires additional memory to store the temporary arrays used in the sorting process, whereas quick sort is an in-place sorting algorithm that does not require additional memory. Depending on the specific requirements of the research project, one algorithm may be more suitable than the other.

The choice of sorting algorithm can have a significant impact on the efficiency and resources required to sort large data sets in scientific research. By understanding the advantages and disadvantages of different sorting algorithms, researchers can make informed decisions about which algorithm to use in different scenarios.

Conclusion

Sorting algorithms play a crucial role in computer science and are used in many real-life applications. Whether it's sorting names in a phone book, movies or songs by popularity/release date, or large amounts of data in data analytics, sorting algorithms help us find information easily and more efficiently. An efficient sorting algorithm can significantly improve the performance of these tasks. From the simplest sorting algorithms like bubble sort and insertion sort to the more complex ones like quick sort and merge sort, it's important to understand the basics of sorting algorithms and how to apply them in solving real-world problems through code. Whether you're a beginner or an experienced programmer, understanding sorting algorithms will help you become a better problem-solver and equip you with the skills to tackle complex programming challenges.