NumPy Binomial Distribution

Definition of Binomial Distribution

The binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent Bernoulli trials, each with the same probability of success. It is commonly used in fields such as finance, biology, and quality control. Understanding this distribution helps us predict the probability of obtaining a certain number of successes in a given number of trials, laying the foundation for more complex statistical analyses.

Importance of Binomial Distribution in Probability Theory

The binomial distribution is important in probability theory because it models independent trials with fixed success or failure outcomes. Many real-life scenarios, such as flipping a coin or conducting a series of medical tests, can be viewed as a series of independent trials. The binomial distribution helps determine the probability of a specific number of successes occurring in a fixed number of trials with a known probability of success.

For instance, if we want to study the number of heads obtained when flipping a fair coin 10 times, each flip can be considered an independent trial with two possible outcomes: success (heads) or failure (tails). The binomial distribution can then be used to calculate the probability of obtaining a specific number of heads, such as 5.

Understanding Probability Mass Function (PMF) in NumPy Binomial Distribution

A Probability Mass Function (PMF) measures the probability of each possible outcome of a discrete random variable. In the context of the NumPy binomial distribution, the PMF provides a way to understand the likelihood of obtaining a certain number of successes in a fixed number of trials. Using NumPy, we can generate and analyze binomial distributions and gain insight into the probabilities of different outcomes.

What is a Probability Mass Function?

A Probability Mass Function (PMF) is a mathematical function that gives the probability distribution for a discrete random variable. It assigns probabilities to each possible outcome of the random variable. The PMF of a binomial distribution is computed using the binomial coefficient, representing the number of ways to choose a certain number of successes from a given number of trials. The formula for the binomial coefficient is:

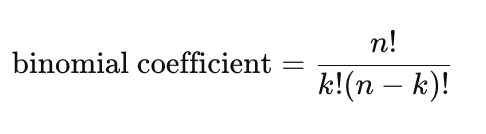
where nnn is the number of trials, and kkk is the number of successes. The PMF is then calculated by multiplying the binomial coefficient by the probability of success raised to the power of the number of successes and the probability of failure raised to the power of the difference between the number of trials and the number of successes.

How to Calculate PMF in NumPy Binomial Distribution

To calculate the PMF in the NumPy binomial distribution, use the binom.pmf function from the SciPy library. This function allows us to define values for the number of trials, probability of success, and sample size.

Step 1: Import the necessary libraries:‍


import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

Step 2: Define the parameters for the binomial distribution:‍


n = 10  # number of trials
p = 0.5  # probability of success
size = 1000  # sample size

Step 3: Calculate the PMF using the pmf method from the binom distribution:

x = np.arange(n + 1)  # possible outcomes
pmf = stats.binom.pmf(x, n, p)  # calculate PMF

Step 4: Visualize the results using a bar plot:‍


plt.bar(x, pmf)
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.title('Probability Mass Function of Binomial Distribution')
plt.show()

Following these steps, we can calculate the PMF in the NumPy binomial distribution and visualize it using a plot.

Examples of PMF Calculations Using NumPy

To calculate the PMF using NumPy:

Step 1: Import the necessary libraries:

import numpy as np
from scipy.stats import binom

Step 2: Define the values for the binomial distribution:‍


n = 10
p = 0.5
values = np.linspace(0, n, n + 1)

Step 3: Calculate the PMF using the binom.pmf function:‍


pmf = binom.pmf(values, n, p)
print(pmf)

This code will display the PMF values for the specified binomial distribution.

Exploring Output Shape in NumPy Binomial Distribution

Determining the Shape of the Output Array

To determine the shape of the output array, examine the dimensions and sizes of the input arrays. The number of dimensions in the input arrays corresponds to the number of axes in the output array. Each dimension represents a specific axis along which the elements are distributed.

If the input arrays have compatible dimensions and sizes, the output array will have the same size along each axis. If not, broadcasting may occur, where the smaller array is repeated or stretched to match the size of the larger array along certain axes.

Visualizing Output Shape with Examples

To visually represent the output shape in Python, use plotting libraries such as Matplotlib. For example, to visualize a histogram of a list of numbers:‍


import matplotlib.pyplot as plt

data = [1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8]
plt.hist(data)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

To visualize a scatter plot showing the relationship between two variables:‍


import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]

plt.scatter(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

Impact of Input Parameters on Output Shape

The input parameters, such as size, scale, rotation, and color, influence the resulting shape output. Size affects the appearance, scale relates to the proportion of the shape, rotation determines orientation, and color impacts visual appeal.

For example, increasing both size and scale results in a larger shape, while changing the rotation angle introduces a sense of movement. Altering the color scheme can change the mood and perception of the shape.

Generating Random Samples with NumPy Binomial Distribution

Generating Random Samples Using NumPy Functions

To generate random samples using NumPy functions, use the numpy.random.binomial function. This function generates random samples from a binomial distribution by specifying parameters such as the number of trials and probability of success.

For example, to generate random samples from a binomial distribution with 10 trials and a probability of success of 0.5:‍


import numpy as np

samples = np.random.binomial(n=10, p=0.5, size=1000)

Controlling Sample Size and Seed for Reproducibility

To control sample size and seed for reproducibility, specify the sample size and set a seed value. The sample size determines the number of observations, while the seed value ensures consistent and reproducible randomization.

For example, to generate a sample size of 1000 and set a seed value for reproducibility:‍


import numpy as np

np.random.seed(42)
samples = np.random.binomial(n=10, p=0.5, size=1000)

Analyzing Random Samples for Statistical Inference

Analyzing random samples for statistical inference involves selecting a random sample, determining an appropriate sample size, and conducting statistical tests. Common statistical tests include t-tests, chi-square tests, correlation analyses, and regression analyses.

For example, to analyze the random samples generated:‍


import numpy as np
import scipy.stats as stats

n = 10
p = 0.5
samples = np.random.binomial(n, p, 1000)
mean = np.mean(samples)
std_dev = np.std(samples)

Comparing Binomial Distribution with Normal Distribution in NumPy

In NumPy, we can compare the binomial distribution and the normal distribution by examining their similarities and differences.

The binomial distribution is characterized by the parameters nnn (number of trials) and ppp (probability of success), while the normal distribution is described by its mean (μ) and standard deviation (σ). A key similarity is that the binomial distribution can be approximated by the normal distribution under certain conditions. As the number of trials increases and the probability of success remains moderate, the binomial distribution becomes more bell-shaped and can be approximated by the normal distribution.

To generate random numbers from both distributions using NumPy:‍


import numpy as np

# Binomial distribution
binomial_samples = np.random.binomial(n=10, p=0.5, size=1000)

# Normal distribution
normal_samples = np.random.normal(loc=0, scale=1, size=1000)

By comparing these functions and their outputs, we can better understand the similarities and differences between the binomial and normal distributions in NumPy.